3.6 Sinusoidal Function Transformations
4 min read•january 28, 2023
Kashvi Panjolia
Kashvi Panjolia
AP Pre-Calculus 📈
resourcesSee Units
We know that all sinusoidal functions -- functions that look like the sine curve -- have certain common characteristics. We qualitatively defined amplitude, period, frequency, midline, and other terms in the last guide, and now we are going to define them quantitatively. We will learn new terms as well, and focus on how they all connect through the equation for a sinusoidal function. By the end of this guide, you will know this equation inside and out, and be able to get loads of information from it.
The Equation
The equation for a sinusoidal function that is based on the sine curve is
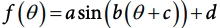
Image courtesy of CollegeBoard.
The equation for a sinusoidal function that is based on the cosine curve is
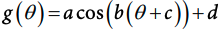
Image courtesy of CollegeBoard.
These equations may look scary at first, but they are really very similar to what you learned in algebra. The main purpose of all the letters in the equation is to show the transformations of the sinusoidal function from the original sine (or cosine) curve. These transformations are vertical stretch/compression, horizontal stretch/compression, vertical shift, and horizontal shift. All the transformations also apply to the cosine curve in the same way, but we will be using sine in this guide for simplicity. Let's go through the equations above one part at a time to discover the plethora of information they contain.
The equation f(θ) = asin(b(θ + c)) + d is made up of four parts: the function f(θ), the variable θ, the trigonometric function sine, and the constants a, b, c, and d. The function f(θ) is the overall function that we are trying to solve. The variable θ is the input to the function, and the output is the value of f(θ). The variable x can also be used to represent the angle in this equation, and the output would become the value of f(x).
The trigonometric function sin, which stands for "sine," is a mathematical function that takes an angle and returns the sine of that angle. In this equation, the sin function is applied to the expression b(θ + c), which is inside the parentheses.
The constants a, b, c, and d are used to manipulate the equation to fit a specific situation. These constants can be used to change different characteristics of the wave pattern that is being represented by the equation.
Amplitude
The constant "a" represents the amplitude of the wave. The amplitude is the measure of how high the wave is from its resting position, or midline. It is the maximum displacement of a point on the wave from its undisturbed position. When the value of "a" is increased, the amplitude of the wave also increases, making the wave taller. When the value of "a" is decreased, the amplitude of the wave decreases, making the wave shorter.
The "a" value in the equation may be negative, but the amplitude is always positive. If the value for "a" were -7, you would say the amplitude is 7. The negative sign represents a reflection over the x-axis of the wave.
Period
The constant "b" represents the frequency of the wave, or the wavelength of the wave. The frequency of a wave is the number of oscillations (or cycles) that occur in one second, and it is measured in hertz (Hz). The reciprocal of the frequency is the period of the wave, and it is the amount of time it takes for one complete cycle of the wave to occur.
In the case of a sinusoidal function, the period is given by the equation T = 2𝛑/b where T is the period and b is the frequency (or wavelength). This equation states that the period of the sinusoidal function is equal to twice 𝛑 (2𝛑) divided by the frequency (b).
As the frequency (b) increases, the period of the wave decreases, meaning that the wave oscillates more slowly. Conversely, as the frequency (b) decreases, the period of the wave increases, meaning that the wave oscillates more quickly.

Image courtesy of MathIsFun.
Phase Shift
The constant "c" represents the phase shift, or horizontal shift, of the wave. The phase shift is the amount by which the wave is shifted to the left or right. It is the amount of horizontal displacement of the wave. When the value of "c" is increased, the wave is shifted to the right. When the value of "c" is decreased, the wave is shifted to the left.
Vertical Translation
The constant "d" represents the vertical shift of the wave. The vertical shift is the amount by which the wave is shifted up or down. It is the amount of vertical displacement of the wave. When the value of "d" is increased, the wave is shifted upward. When the value of "d" is decreased, the wave is shifted downward.
Below is an image showing how the equation for a sinusoidal function can be constructed from a graph:

Image courtesy of MathIsFun.
Practice Problems
1. What is the amplitude of the wave represented by the equation f(θ) = 3sin(2(θ+1)) + 5?
a) 3
b) 2
c) 5
d) 1
Answer: a) 3
2. What is the wavelength of the wave represented by the equation f(θ) = 2sin(0.5(θ-2)) + 3?
a) 2π
b) 4π
c) 0.5π
d) 1π
Answer: c) 0.5π
3. What is the phase shift of the wave represented by the equation f(θ) = 4sin(3θ+1.5)) - 2?
a) 0.5
b) -2
c) 3
d) 1.5
Answer: a) 0.5
Note: For this problem, there is a 3 in front of the θ inside the parentheses. To find the "c" value, or the phase shift, we need to factor out the 3 so that we get θ by itself. By factoring out the 3 from 1.5, we found the phase shift to be 0.5.
Browse Study Guides By Unit
🥑Unit 3 – Trigonometric & Polar Functions

© 2023 Fiveable Inc. All rights reserved.