Peter Apps
Peter Apps
AP Physics 1 🎡
257 resourcesSee Units
Enduring Understanding 6.A
A wave is a travelling disturbance that transfers energy and momentum.
Essential Knowledge 6.A.1
Waves can propagate via different oscillation modes such as transverse and longitudinal.
Essential Knowledge 6.A.2
For propagation, mechanical waves require a medium.
Essential Knowledge 6.A.3
The amplitude is the maximum displacement of a wave from its equilibrium value.
Essential Knowledge 6.A.4
Classically, the energy carried by a wave depends on and increases with amplitude. Examples include sound waves.
Anatomy of a Wave
A wave is a periodic disturbance, meaning that it repeats over and over in a predictable pattern. The disturbance can cause the particles of the material the wave is propagating through to vibrate either perpendicular or parallel to the direction of the wave’s motion.
If the particles vibrate parallel to the direction of motion, the wave is longitudinal. If they vibrate perpendicular, the wave is transverse.
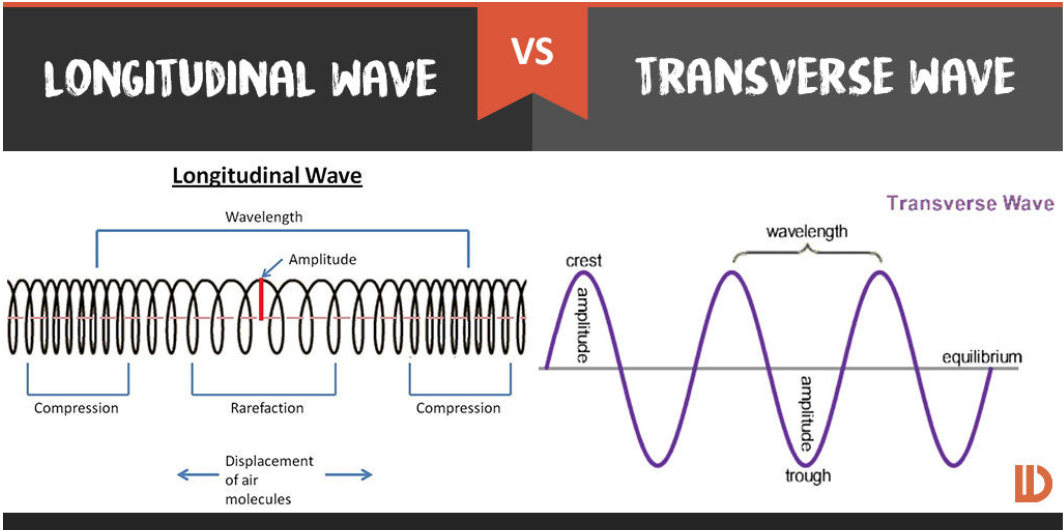
Image courtesy of Difference.Wiki.
Both types of waves have similar features:
Amplitude
- The height of the wave, measured from the equilibrium position.
- The amplitude also describes the amount of energy a wave transfers. The higher the amplitude, the larger the energy.
Wavelength
- The distance from one repeated unit to the next.
- On a Longitudinal wave this is from compression to compression or rarefaction to rarefaction.
- On a Transverse wave this is from crest to crest, or trough to trough.
Period - the time it takes for one cycle of a wave to occur
Frequency - the number of cycles of a wave in a given amount of time
Velocity of a Wave
The velocity of a wave depends on the medium (material) that the wave is traveling through. In AP 1, we only deal with mechanical waves that require a medium to travel through (they can’t travel through empty space which is a vacuum). If you go ahead and take AP 2, you’ll learn about Electromagnetic waves that can travel through empty space. In general terms, mechanical waves travel faster through denser materials, or when the tension in the material is greater. You can mess around with this concept by taking a look at the PhET Waves on a String simulation.
Since velocity is distance / time, we can apply the same idea to finding the velocity of a wave. The distance a wave travels is its wavelength, and the time it takes to travel that distance is the period. Combining these together we get two equations, one with period and one with frequency (remember T=1/f).
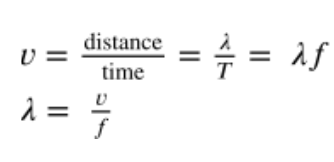
(or written like the Reference Table)
As long as the velocity of the wave remains constant (the material or tension doesn't change) we can see an inverse relationship between wavelength and frequency. A lower frequency means a larger wavelength and vice versa.
Sample Question (AP Classroom)
A transverse wave travels to the right along a string.
a. Two dots have been painted on the string. In the diagrams below, those dots are labeled P and Q.
i. The figure below shows the string at an instant in time. At the instant shown, dot P has maximum displacement and dot Q has zero displacement from equilibrium. At each of the dots P and Q, draw an arrow indicating the direction of the instantaneous velocity of that dot. If either dot has zero velocity, write "v = 0" next to the dot.
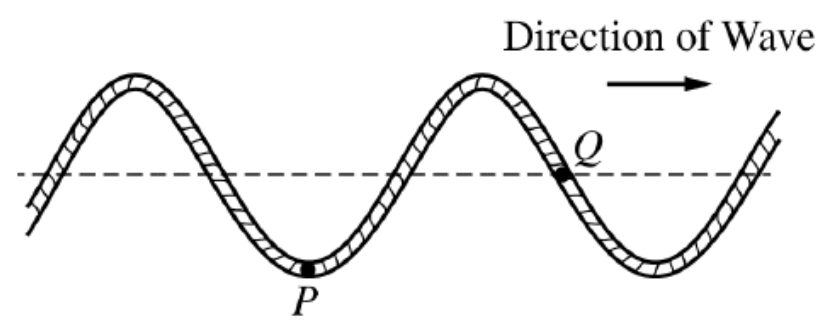
ii. The figure below shows the string at the same in stant as shown in part (a)i. At each of the dots P and Q, draw an arrow indicating the direction of the instantaneous acceleration of that dot. If either dot has zero acceleration, write "a = 0" next to the dot.
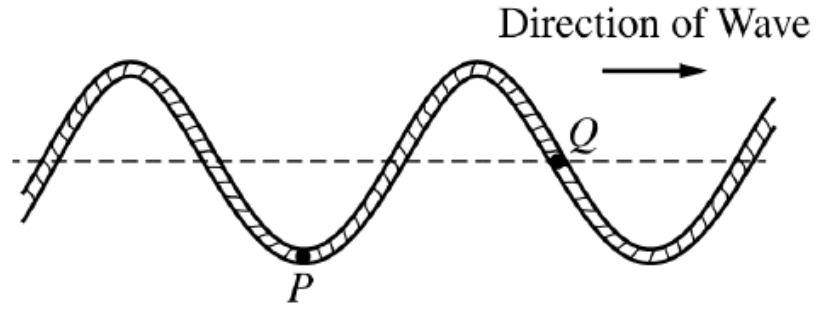
b. The figure below represents the string at time t = 0 the same instant as shown in part (a) when dot P is at its maximum displacement from equilibrium. For simplicity, dot Q is not shown.
i. On the grid below, draw the string at a later time t = T/4, where T is the period of the wave.
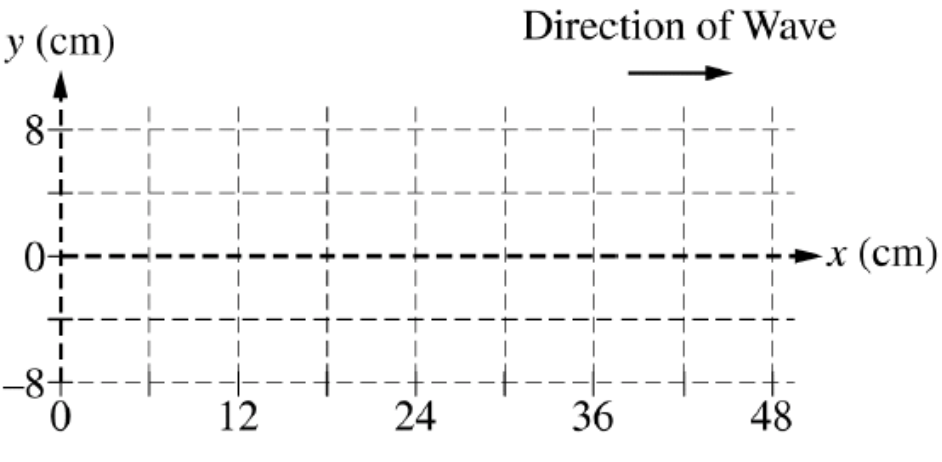
ii. On your drawing above, draw a dot to indicate the position of dot P on the string at time t = T/4 and clearly label the dot with the letter P.
c. Now consider the wave at time t = T. Determine the distance traveled (not the displacement) by dot P
between times t = 0 and t = T.
Answer:
a) i.
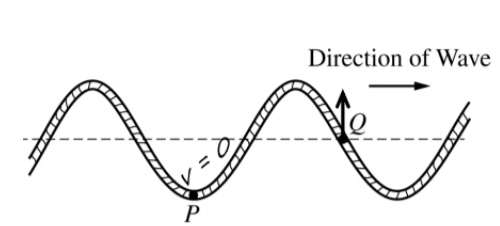
At point P, the wave it at it’s lowest point so the point is not moving down or upwards at that time. At point Q, the particle is moving upwards to reach the top of the incoming crest in the next instant of time.
ii.
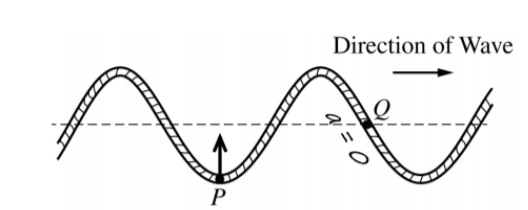
At point P, the particle is at the furthest distance from the equilibrium point which means that the force and acceleration on it must be at a maximum (very similar to mass on a spring from SHM Unit 6). Point Q is on the equilibrium point, so there is no net force or acceleration acting at that point.
b)i and ii.
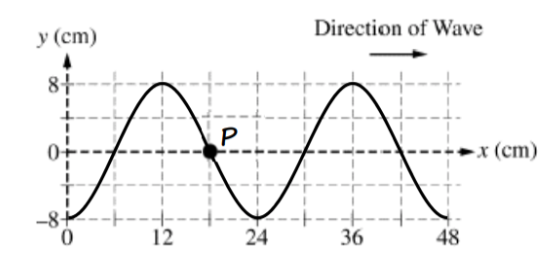
Because the particle at point P must complete a full cycle of the wave in time T, time T/4 means that the particle must move ¼ of a cycle towards the right. So since the wavelength of the wave is 24cm, shift each part of the wave 6cm to the right. Point P was at 18cm in the previous diagram and doesn’t move with the wave (waves transfer energy and momentum not mass) it will be in the same x location.
c) The particle at point P travels a complete cycle of the wave (from -8 to 8, then back to -8cm) for a total vertical distance of 32cm. It does not move horizontally at all.
🎥Watch: AP Physics 1 - Unit 10 Streams
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
👉AP Physics Essentials
🧐Multiple Choice Questions (MCQs)
✍️Free Response Questions (FRQs)
📆Big Reviews: Finals & Exam Prep

© 2023 Fiveable Inc. All rights reserved.